応力とひずみ
目次
応力とは
応力とは、その部材内に発生している単位面積あたりの力である。単位面積あたりの力とは、ここでは1㎟（平方ミリメートル）あたりにかかる力のことである。
例えば、断面積が10㎟の棒を100Nの力で引っ張ると、そのときに棒に発生している単面積あたりの力（応力）は下記のような計算式になる。
$$ 応力(シグマ)σ=\frac{引っ張る力P}{棒の断面積A}=\frac{100N}{10㎟}=10N/㎟$$
応力はσ(シグマ)の記号を使います。
荷重の伝達
図1：荷重の伝達
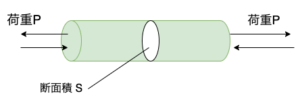
図1のように、棒の両端に大きさがPの荷重が作用している。このとき、ある面に対して外側に、その面を引っ張る方向に作用する荷重のことを引張荷重と呼び、その面を押しつける方向に作用する荷重のことを圧縮荷重と呼ぶ。
この棒に作用する引張荷重や圧縮荷重は軸力とも呼ばれる。
図2：引張荷重と内力
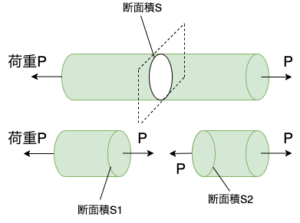
図2より、棒に両端に大きさが同じ荷重Pが互い違いに逆向きに作用している。この棒に対する外力の和は０であるので、この棒における力の釣り合いは保たれている。この棒の内部において棒の長さ方向に垂直な断面Sを考える。（横断面S）
この横断面Sの部分で棒を切断したと仮定すれば、２つの切断面S1及びS2には同じく大きさPの荷重が作用して、切断された左右２つの棒においても力の釣り合いは保たれる。つまり、図2のように両端に逆向きの荷重を受ける棒の内部の力の作用を考えたとき、外力が伝達されるように棒をどの部分で切断しても同じ大きさの荷重Pが棒の内部に作用する力（内力）として作用することがわかる。
つまり、物体が動かずに静止しているということは、このように、物体にかかっている力の合力が０で釣り合っている状態である。一見動かないから、その物体には力がかかっていないように思えるかもしれないが、実際には、物体の内部と外部に力がかかっており、その合力が０であるということなのである。
垂直応力と圧縮応力
図3：引張荷重と応力
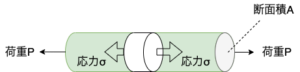
図3より、棒の両端に引張荷重が作用している場合について考える。棒の両端に作用する荷重Pと棒の断面積Aから、単位面積あたりに作用する力（応力）σを考えると、
$$応力：σ=\frac{荷重P}{断面積A}=\frac{P}{A}$$
となる。
ここで、荷重の単位はN(ニュートン)、断面積の単位は㎡であるので、応力の単位は、N/㎡となり、物体の表面や物体の内部における任意の断面に対して、単面積あたりに作用する力として定義することができる。応力作用する面に対して垂直方向に作用する応力のことを垂直応力と呼ぶ。
図4：垂直応力
図4のように応力の作用面を垂直に引っ張る方向の働く応力を引張応力と呼び、面に対して垂直に押しつける方向に働く応力を圧縮応力と呼ぶ。
せん断応力
図5 :せん断力とせん断応力
図5より、ある面に対して、平行で同時に互い違いな方向に作用する力をせん断力ととしてQと呼ぶ。このせん断力Qを単面積あたりの力として表したものをせん断応力と呼んでいる。ある面の面積をAとすれば、せん断応力τは次式で定義することができる。
$$せん断応力:\tau=\frac{せん断力Q}{面積A}={Q}{A}$$
図6：せん断応力とせん断ひずみ
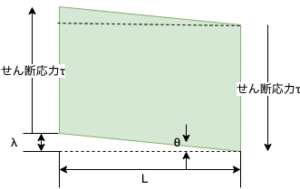
ここで、図6において、基準の長さに対するせん断変形量の比を考えてみる。せん断変形量とは、ここではせん断応力が作用したことによって生じる面のひずみ量のことをいう。図5におけるせん断応力が作用する瞬間の変化のない状態である面(正方形)の一辺の長さをLとして、図6に示されるように、図5における正方形の面と平行な方向への変形量をλとすると、Lとλの比がせん断ひずみとなる。
$$せん断ひずみ:\gamma=\frac{\lambda}{L}$$
このとき、せん断変化量λがLに比べて大変小さければ、これらの長さと角度θの間には次の関係式が成立する。
$$\tan\theta\approx\theta=\frac{\lambda}{L}……①$$
この式から、せん断ひずみはせん断変化量λを角度(rad=ラジアン)で表したものと見なすことができる。なぜならば、図6におけるθが中心角で、かつLを円の弧と見なしてλの量が変化する円と考えた場合。
$$tan\theta=\frac{\lambda}{L}……②$$
と見なすことができ、ここで、λの変化量が大変小さければ、上の式の①と②から
$$tan\theta=\frac{\lambda}{L}\approx\theta$$
と考える事ができるからである。
せん断応力τとせん断ひずみλの間にはフックの法則が成立する。
$$せん断変形に関するフックの法則:\tau=G\lambda (比例定数G:せん断弾性係数)$$
- フックの法則
ばねのような弾性のある物体の伸びと弾性限度以下の荷重は正比例するという法則（弾性の法則）
力は伸びに比例するという法則でであり、荷重は伸びに正比例し、次の式が成立する。
$$F=kx$$
ここでxは自然長からの伸び、または縮みである。自然長とは、荷重のかかっていないばねが自然に停止する位置のことである。
Fはばねにかかる力であり、ばねによる反力である。
kはばね定数と呼ばれる定数であり、ばね固有の値をもち、ばねそのものの強さを示している。