静力学:力の釣り合い
目次
力の釣り合い
力の大きさと方向
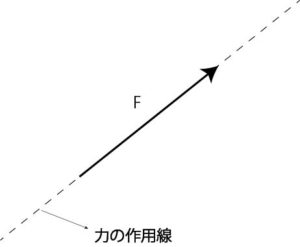
図1:力の大きさと方向
力の合成
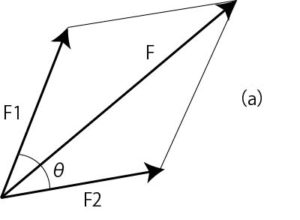
図2(a):力の合成
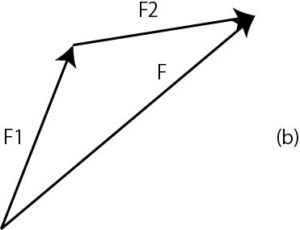
図2(b):力の合成
$$\angle{O’A’B’}=\pi-\theta$$
$$
F^2=F1^2+F2^2-2F1F2cos(\pi-\theta)
$$
$$
cos(\pi-\theta)=-cos\theta より
$$
$$
F^2=F1^2+F2^2+2F1F2cos\theta …式①
$$
F1=15N, F2=10N, θ=50° とするとき、図3(a)に示す2つの力F1、F2の合力の大きさFとF1とのなす角θ1を求めよ。
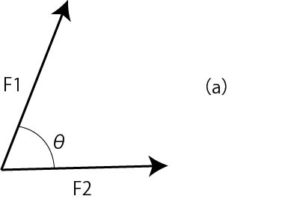
図3(a):合力の大きさと方向
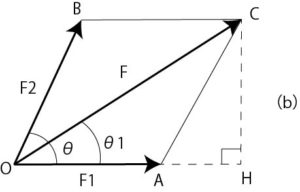
図3(b):合力の大きさと方向
$$
F^2=F1^2+F2^2+2F1F2cos\theta …式①
$$
$$F1=15N, F2=10N, θ=50° を代入すると$$
$$
F^2=15^2+10^2+2\times15\times10\cos50^{\circ}
$$
$$
F=\sqrt{15^2+10^2+2\times15\times10\cos50^{\circ}}
$$
$$\cos50^{\circ}=0.96より$$
$$F=24.8N$$

図3(b):合力の大きさと方向
$$F\sin\theta1=F2\sin\theta…② であるから$$
$$24.8\sin\theta1=10\sin50^{\circ}$$
$$よって \sin\theta1=0.104$$
$$ゆえに \theta1=6^{\circ}$$
例題1をpythonで計算する
先に示した例題をPythonによるプログラミングで解いてみる。
F1=15N, F2=10N, θ=50° とするとき、図3(a)に示す2つの力F1、F2の合力の大きさFとF1とのなす角θ1を求めよ。
- Python3の環境構築はこちら
F1とF2の合力を求める

図3(a):合力の大きさと方向
#標準モジュールmathインポート
import math
# 題意から与えられた変数を定義する
F1 = 15
F2 = 10
# 式①を関数として定義する
def addfoce():
F = F1**2+F2**2+2*F1*F2*math.cos(50)
G = math.sqrt(F) #式①の平方根
return G
print(round(addfoce(), 1)) #小数点以下第一位野までの処理をして結果を出力
# 結果:24.8NF1と合力Fとのなす角を求める
F1=15N, F2=10N, θ=50° とするとき、図3(a)に示す2つの力F1、F2の合力の大きさFとF1とのなす角θ1を求めよ。
- Python3の環境構築はこちら

図3(b):合力の大きさと方向
#標準モジュールmathインポート
import math
# 題意から与えられた変数を定義する
F = 24.8
F2 = 10
# 式②を関数で定義する
def theta():
a = F2*math.sin(50)/F
b = math.degrees(a) #ラジアンから度に変換するのがmath.degrees()
return b
print(round(theta())) #小数点以下を丸めて結果を出力
#結果 6°