Statics: Force balance
Statics is the mechanics that deals with the balance of forces acting on a stationary object. Consider the case where an object is stationary. For example, when an object is placed on a desk, the weight of the object exerts a force, but the desk itself does not move. In such a state, various forces are applied to the object, and it can be said that they are in a balanced state.
Here, I would like to explain about the balance of forces and moments that work when an object is stationary.
table of contents
Balance of power
Force magnitude and direction
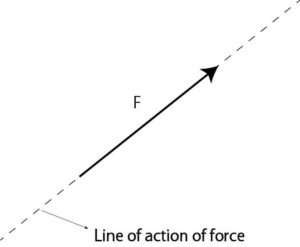
Figure 1: Force magnitude and direction
As shown in FIG. 1, the force is not expressed only by the unit of its magnitude, but is expressed by the vector quantity indicating the direction and magnitude of action. If this vector quantity is expressed as F, F acts in the direction of the arrow with a force as much as the unit of force magnitude. It means that.
Further, from FIG. 1, the dotted line extending before and after the vector representing the force is called the action line of the force, and even if the vector is moved on the action line of the force, the unit of the direction and the amount of the force represented by the vector does not change. ..
Force synthesis
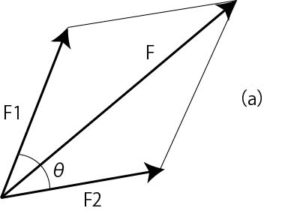
Figure 2 (a): Force synthesis
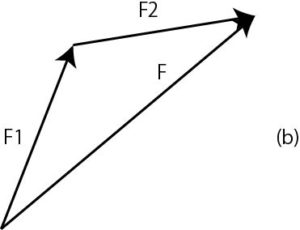
Figure 2 (b): Force synthesis
A vector that combines two or more forces and is represented by one force is called a resultant force. Combining two forces is equivalent to finding the sum of the two vectors.
Assuming that the resultant force of the two forces F1 and F2 is F, the resultant force F is represented as a diagonal line of a parallelogram as shown in FIG. 2 (a). Alternatively, as shown in FIG. 2 (b), it becomes one side (diagonal line) of a triangle as if the parallelogram of FIG. 2 (a) was cut off diagonally.
In FIG. 2 (a), assuming that the angle formed by F1 and F2 is θ, the following relationship is established using the cosine theorem in trigonometric functions.
In the triangle O’A’B’ in Fig. 2 (b), the angle formed by it is
$$\angle{O’A’B’}=\pi-\theta$$
Therefore, in the triangle O’A’B’, F is expressed as follows from the law of cosines.
$$
F^2=F1^2+F2^2-2F1F2cos(\pi-\theta)
$$
$$
cos(\pi-\theta)=-cos\theta Than
$$
$$
F^2=F1^2+F2^2+2F1F2cos\theta …formula①
$$
Since the resultant force is the same vector quantity, it has a magnitude and a direction. Based on the above, let’s solve Example 1.
[Example 1]
When F1 = 15N, F2 = 10N, θ = 50 °, find the angle θ1 between the two forces F1 and F2 shown in Fig. 3 (a).
[Solution]
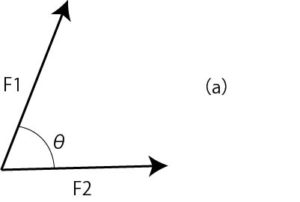
Figure 3 (a): magnitude and direction of resultant force
From the subject, find the magnitude F of the resultant force. From formula ①
$$
F^2=F1^2+F2^2+2F1F2cos\theta …formula①
$$
$$F1=15N, F2=10N, θ=50° Substituting$$
$$
F^2=15^2+10^2+2\times15\times10\cos50^{\circ}
$$
$$
F=\sqrt{15^2+10^2+2\times15\times10\cos50^{\circ}}
$$
$$\cos50^{\circ}=0.96 Than$$
$$F=24.8N$$
Drawing from Fig. 3 (a) to Fig. 3 (b), let θ1 be the angle between F1 and the resultant force F.
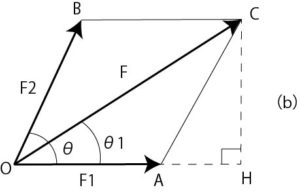
Figure 3 (b): magnitude and direction of resultant force
From the subject, the angle θ1 to be formed is obtained.
$$F\sin\theta1=F2\sin\theta…② Because$$
$$24.8\sin\theta1=10\sin50^{\circ}$$
$$Therefore, \sin\theta1=0.104$$
$$therefore \theta1=6^{\circ}$$
Calculate Example 1 with python
Let’s solve the above example by programming with Python.
[Example 1]
When F1 = 15N, F2 = 10N, θ = 50 °, find the angle θ1 between the two forces F1 and F2 shown in Fig. 3 (a).
- Click here to build the environment for Python3
Find the resultant force of F1 and F2

Figure 3 (a): magnitude and direction of resultant force
#Standard module math import
import math
# Define a variable given by the subject
F1 = 15
F2 = 10
# Define expression ① as a function
def addfoce():
F = F1**2+F2**2+2*F1*F2*math.cos(50)
G = math.sqrt(F) #Square root of equation ①
return G
print(round(addfoce(), 1)) #Process up to the first decimal place and output the result
# Result:24.8N
Find the angle between F1 and the resultant force F
[Example 1]
When F1 = 15N, F2 = 10N, θ = 50 °, find the angle θ1 between the two forces F1 and F2 shown in Fig. 3 (a).
- Click here to build the environment for Python3

Figure 3 (b): magnitude and direction of resultant force
#Standard module math import
import math
# Define a variable given by the subject
F = 24.8
F2 = 10
# Define expression ② with a function
def theta():
a = F2*math.sin(50)/F
b = math.degrees(a) #Converting from radians to degrees is math.degrees ()
return b
print(round(theta())) #Round the decimal point and output the result
#Result 6°






