歯車とは

2つの円筒面に互いに刻んだ歯のかみ合いによって回転運動を伝達する機構を歯車機構と呼ぶ。
この機構は、大きな動力を確実に伝達することができるので、回転の増速や減速、トルクの拡大、回転方向の変換などに利用されている。ここでは、この歯車の種類と歯の大きさを表すモジュール。歯車の角速度比を一定に保つ歯形曲線とインボリュート波形の性質などについて解説していく。
この解説を通して、種々の歯車列の角速度比の解析法と、減速機や差動歯車装置の仕組みに関する理解ができればと思う。また、歯車機構の知識は、自動車や産業機械などの構造に関する仕組みを理解し、それらの開発や機能の応用、分解整備や修理に関する基礎知識となるので、是非とも学習しておくことをおすすめする。
目次
歯車の構成
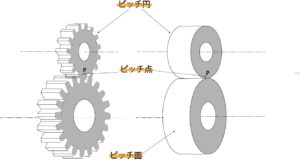
図1:歯車と摩擦車
例えば、ベルト駆動などの摩擦車は、静かで滑らかで構造が簡単、かつ、コストパフォーマンスに優れているなどの利点があるが、滑りが発生するので大きなトルクを伝達することができず、回転数比が不正確で、摩擦面の摩耗や変質が起こりやすくなる。その滑りを少なくするために接触力を大きくすれば、軸受けの損傷や摩擦面の変形による半径変化が起こってくる。これらの問題を解決するために図1のように摩擦車の摩擦面に歯を刻んで、歯のかみ合いによって回転を確実に伝達することができるようにしたものが歯車である。
この歯車のメリット、デメリットをまとめると次のようになる。
- 歯車のメリット
- 大きなトルクを伝達できる。
- 回転比(ギヤ比)が一定で正確にできる。
- 軸受にかかる負荷が小さくて済む。
- 歯車のデメリット
- 歯と歯の間にガタ(バックラッシュ)が発生する。
- 騒音が発生しやすい。
- 形状が複雑、加工が困難であるので、コストパフォーマンスが悪い。
歯車の各部名称

図1:歯車と摩擦車
1対の歯車がかみ合っているとき、その歯車と同じ運動をする摩擦車の表面に相当する面(歯車の歯先を軸方向の正面から見た面)をピッチ面と呼ぶ。
1対の歯車がかみ合っているとき、それに相当する摩擦車の外周円に相当する歯車の円をピッチ円と呼ぶ。
1対の歯車がかみ合っているとき、その2つの歯車と同じ運動をする2つ摩擦車の接触点に相当する点(歯車の歯のかみ合い点)をピッチ点と呼ぶ。
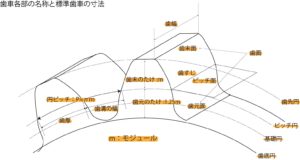
図2-1:歯車各部の名称と標準歯車の寸法その1
- 図2-1より歯車各部の名称
- 歯先円:歯先を通る円
- 歯底円:歯底を通る円
- ピッチ円:図1の摩擦車に相当する円がピッチ円となり、歯先円と歯底円の間にある円をいう。
- 歯元のたけ:ピッチ円より内側の歯の高さ
- 歯末のたけ:ピッチ円より外側の歯の高さ
- 全歯たけ:歯全体の高さ
- 歯面:歯のかみ合う面
- 歯幅:軸方向の歯の長さ
モジュールと圧力角
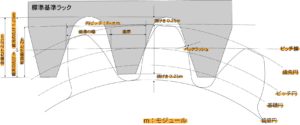
図2-2:歯車各部の名称と標準歯車の寸法ぞの2
歯の寸法を表す基準としてモジュールが用いられる。ピッチ円直径をd(mm)、歯数をzとすればモジュールm(mm)は次のように定義される。
$$ m=\frac{d}{z} $$
モジュールmの値はJIS規格で規定されている。一般的に使われる標準寸法の歯(並歯)では、歯末のたけはモジュールに等しく、歯元のたけは、かみ合わせた相手の歯車の歯先との間に隙間(頂げき)を設けるために1.25m以上とすることが定められている。
歯のかみ合いに寄与する有効歯たけは、歯末側がm、歯元側がmで合計2mとなる。
また、ピッチ円上における隣り合う2つの歯の間隔pを円ピッチと呼び、ピッチ円の円周を歯数で割ることにより求められる。
$$ p=\frac{πd}{z}=πm $$
このように、歯の大きさや間隔は、すべてモジュールを基準にして決定される。
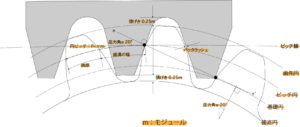
図2-3:歯車各部の名称と標準歯車の寸法ぞの3
また、ピッチ円上の歯と溝の部分の長さをそれぞれ歯厚、歯溝の幅と呼ぶ。歯車を隙間なくかみ合わせるためには、歯厚と歯溝の幅は円ピッチpの半分ずつとする必要があるが、実際には加工誤差による歯の干渉を避けるためにわずかの「あそび」を入れるように設計される。これをバックラッシュと呼ぶ。
すなわち、歯溝の幅のほうが歯厚よりわずかに大きくなる。
また、歯面の傾きを表す量として圧力角がある。圧力角αは、2つの歯車の接触点での共通法線と、歯の運動方向(2つのピッチ円の接点での共通接線の方向)のなす角として定義されていて、JIS規格では標準歯車の圧力角は20°と定められている。
このように、歯車の歯の大きさ、間隔、形状はモジュールmと圧力角αを基準に定められ、モジュールと圧力角が等しい歯車はかみ合う。
以下にモジュールの標準値と歯の大きさを示す。

図3:モジュールの標準値と歯の大きさ
歯車の種類
数多い歯車の種類は、2つの歯車軸の相対的な位置関係によって大きく3つに分類することができる。
平行軸
平行軸の歯車の対になる歯車には、円筒面に歯を付けた円筒歯車が用いられる。
その中で最も一般的なのが、平歯車であり、歯すじが回転軸に対して平行になっている。
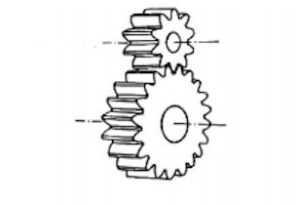
図4-1:平歯車
平歯車は政策が容易であり、最も多く用いられている歯車である。
一般的に、円筒面の外側に歯を持つものを外歯車、円筒面の内側に歯を持つものを内歯車という。
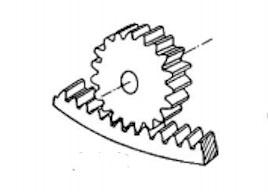
図4-2:内歯車
また、大きさの異なる2つの歯車がかみ合っているとき、大きい方の歯車をギヤ(大歯車)、小さい方の歯車をピニオン(小歯車)と呼ぶ。
ギヤ(大歯車)の直径を無限に大きくしていくと想定したとき、歯が直線上に並んだ歯車となり、これをラックと呼んでいる。
ラックとピニオンの組み合わせにより直線運動と回転運動を互いに変換することができる。

図4-3:ラック
歯すじが回転軸に対して平行でない状態に加工されている歯車には、はずば歯車や、やまば歯車がある。
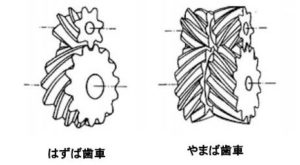
図4-4:はずば歯車とやまば歯車
はずば歯車ややまば歯車は平歯車より強度が高く、1つの歯から次の歯への移り変わりが滑らかになり、振動や騒音が減少するため、高速回転などの用途用いられることが多い。
交差軸
2軸が互いに交わる場合には、円錐面に歯を付けたかさ歯車が用いられる歯すじが曲線であるすぐばかさ歯車、歯すじが曲線であるまがりばかさ歯車がある。
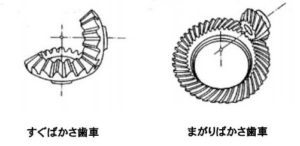
図4-11:すぐばかさ歯車とまがりばかさ歯車
かさ歯車の円錐角を90°にしたモノを、冠歯車と呼ぶ。
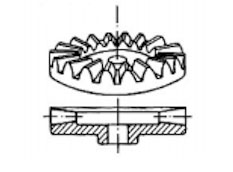
図4-6:冠歯車
食い違い軸
2軸が交わらず平行でもない場合を食い違い軸と呼ぶ。
2軸の角度が直角の場合には、ネジのような形状のウォームとそれにかみ合うウォームホイールによって回転を伝達することができる。この組み合わせをウォームギヤと呼んでいる。
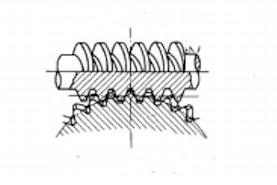
図4-9:ウォームギヤ
ウォームギヤは大きな角速度比を得ることができるが、ウォームホイールからウォームへの回転伝達はできない。
また。2軸が直角でない場合の回転を伝える歯車には、はずば歯車、まがりばかさ歯車をそれぞれ食い違い軸に用いたねじ歯車、ハイポイドギヤなどがある。
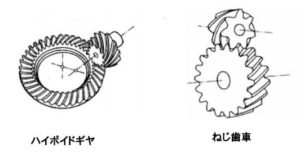
図4-10:ねじ歯車とハイポイドギヤ
歯車の歯形曲線
歯車の歯形曲線には。回転を滑らかに伝えるための仕組みがある。
- 歯車の歯は。接触点が滑りながら一定の角速度比で回転を伝える。
- インボリュート歯車は、どのような歯数を組み合わせても角速度比が一定である。
歯車のかみ合い
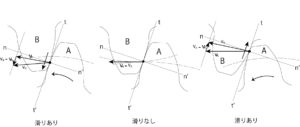
図5:歯車の接触
歯車の1つの歯のかみ合い方を見てみると、接触点歯形曲線に沿って滑りながら回転を伝えていることが理解できる。図5は接触点における歯車A,Bの速度
$$\upsilon{_A},\upsilon{_B}$$
と,Aに対するBの滑り速度
$$\upsilon{_B}-\upsilon{_A}$$
を示している。
滑り速度は、接触点での共通接線
$$t-t’$$
に対して平行である。
歯形曲線状での接触点の軌跡(図5のグレー線)は、歯末側の方が歯元側より長く(ピッチ線を境界にする)、歯末側の接触点が相対的に速く動く。
接触点がピッチ円上にあるときには、
$$\upsilon{_A}-\upsilon{_B}$$
となり、滑りが無くなった状態となる。
この滑り接触の間に歯車の角速度が変化しないように、角速度比一定の条件を満たすように歯形曲線が設計されている。
歯形曲線として最もよく用いられている曲線がインボリュート曲線である。

図5:歯車の接触
インボリュート曲線
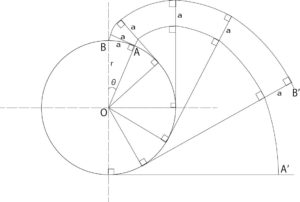
図6:インボリュート曲線と法線ピッチ
図6のように円に巻き付けた糸をたるませないようにほどいていくとき、その糸の先端が描く軌跡をインボリュート曲線と呼び、糸を巻き付けた円を基礎円と呼ぶ。
図6の曲線AA’, BB’は同じ基礎円の巻き付けた糸をそれぞれA,Bからほどいていったときの先端点の軌跡である。この軌跡の線がインボリュート曲線である。
$$\stackrel{\frown}{AB}=α=rθ$$
としたとき次の性質がある
- 2本のインボリュート曲線と糸はどの位置でも垂直に交わり、インボリュート曲線間の距離はどの位置でもαに等しい.この距離αを法線ピッチと呼んでいる。
- インボリュート曲線AA’を基礎円の中心Oの周りにθだけ回転させるとBB’に重なる。すなわち2本のインボリュート曲線は合同であると言える。
例えば、図7に示す半径αの基礎円を持つインボリュート曲線の方程式を次の2つの方法で表すとする。
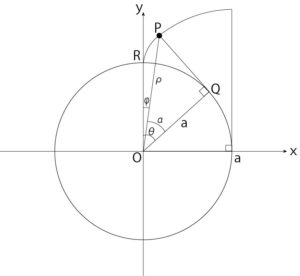
図7:インボリュート曲線
- 点Pの座標\((x, y)\)を\((α, θ)\)を用いて表す。
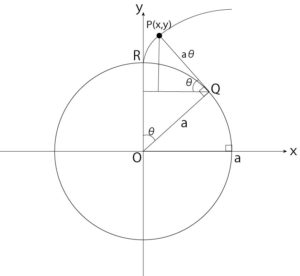
図7-a:点Pの座標(x,y)をa,θで表す
図7-aより
$$\vec{OP}=\vec{OQ}+\vec{QP}…..①$$
\(\triangle{OQS}において線分ABの長さがa\)であることから
$$\vec{OQ}=\begin{pmatrix}a\sin\theta \\ a\cos\theta \end{pmatrix}$$
また、\(\triangle{TQP}\)において線分\(QP=弧\stackrel{\frown}{QR}\)とみなし、その長さは\(a\theta\)であるから
$$QP=\stackrel{\frown}{QR}=a\theta$$
よって、\(\triangle{TQP}\)において線分\(QP=a\theta\)となり
$$\vec{QP}=\begin{pmatrix}-a\theta\cos\theta \\a\theta\sin\theta \end{pmatrix}$$
と表せる。
①より
$$∴\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}a\sin\theta-a\theta\cos\theta \\a\cos\theta+a\theta\sin\theta \end{pmatrix}$$
- 点Pの極座標\((\rho, \phi)\)を\(a, α\)を用いて表す。
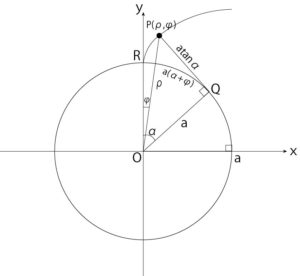
図7-b:点Pの極座標(ρ,φ)をa,αで表す
図7-bの\(\triangle{OQP}\)において
$$\rho\cos\theta=\alpha$$
$$∴\rho=\frac{\alpha}{\cos\alpha}$$
弧\(\stackrel{\frown}{QR}\)の長さ=線分\(QP\)とできるので
$$\stackrel{\frown}{QR}=QP$$
つまり
$$a(\alpha+\phi)=a\tan\alpha$$
$$\phi=\tan\alpha-\alpha$$
よって
$$∴\begin{pmatrix}\rho\\\phi\end{pmatrix}=\begin{pmatrix}\frac{\alpha}{\cos\alpha}\\\tan\alpha-\alpha\end{pmatrix}$$
また、\(inv(\alpha)=\tan\alpha-\alpha\)はインボリュート関数と呼ばれている。
注:図7-aにおいて線分\(QP=弧\stackrel{\frown}{QR}\)とできる理由は、点Qを固定して点Pを点Rへと近づけて行ったとき線分QPの長さが、弧QRの長さ\((=\alpha\theta:弧度法)\)に限りなく近づくからである。近似的に線分\(QP=弧\stackrel{\frown}{QR}\)とすることができる。
インボリュート歯車
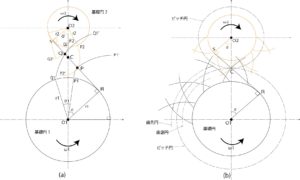
図8:インボリュート歯形による伝動
インボリュート曲線を歯形に持つ2つの歯車を接触させながら回転させると、角速度比は一定になる。このことは図8を参照にして次のように確認することができる。
- 図8-aのように2つの円\(O{_1},O{_2}\)に糸をS字にたわみ無くかける。
- 点Pで糸を切り、円\(O{_1},O{_2}\)を基礎円としてインボリュート曲線\(P{_1}-P{_1′},Q{_1}-Q{_1′}\)を描く。
- 再び糸をつないで、円\(O{_1},O{_2}\)を回転させて糸を点Pから点Qまで送る。
- 点Qで糸を切り、円\(O{_1},O{_2}\)を基礎円としてインボリュート曲線\(Q{_1}-Q{_1′},Q{_2}-Q{_2′}\)を描く。
このとき、インボリュート曲線\(P{_1}-P{_1′}\)と\(P{_2}-P{_2′}\)を接触させながらそれぞれの基礎円と共に回転させれば、曲線は\(Q{_1}-Q{_1′}\)と\(Q{_2}-Q{_2′}\)に一致して、接触点は直線RS上をPからQへと移動する。
ここで各基礎円のの回転角を\(\theta{_1},\theta{_2}\)とすれば次の関係が成り立つ。
$$\stackrel{\frown}{P{_1}Q{_1}}=PQ=r{_1}\theta{_1}=r{_2}\theta{_2}$$
$$∴\frac{\theta{_2}}{\theta{_1}}=\frac{r{_1}}{r{_2}}$$
接触点における共通法線はつねに直線RSとなる。
したがって、接触点の共通法線と円の中心をを結ぶ直線\(O{_1}O{_2}\)は定点Cで交わり、角速度比一定の条件を満たす。
$$\frac{\omega{_2}}{\omega{_1}}=\frac{O{_1}C}{O{_2}C}=\frac{r{_1}}{r{_2}}(一定)$$
したがって、図8-bのようにインボリュート曲線の一部を歯形曲線とする歯車を作れば、角速度比が一定の回転が続くことになる。
このような歯車をインボリュート歯車と呼ぶ。
また、\(O{_1}C,O{_2}C\)を半径とする円をピッチ円とすれば、以下の3つの伝動はすべて同じになることがわかる。
- 基礎円に糸をS字にかけたときの巻き掛け伝動
- ピッチ円による転がり伝動
- インボリュート曲線を歯形とした歯車の接触伝動

図8:インボリュート歯形による伝動
サイクロイド歯車
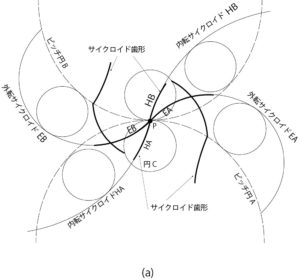
図9-a:サイクロイド歯形による伝動
円上や直線上をもう一つの他の円が転がるとき、転がり円上の一点が描く軌跡をサイクロイド曲線と呼んでいる。
円の外側を転がる場合を外転サイクロイド、円の内側を転がる場合を内転サイクロイドという。
図9-aのように円A,Bをそれぞれ歯車A,Bのピッチ円とし、接触点をPとする。
小円Cを点Pからピッチ円A,Bに沿って転がすとき、外転サイクロイドをEA,EB,内転サイクロイドをHA, HBとする。
EAを歯先、HAを歯元とする歯車と、EBを歯先、HBを歯元とする歯車をサイクロイド歯車と呼ぶ。
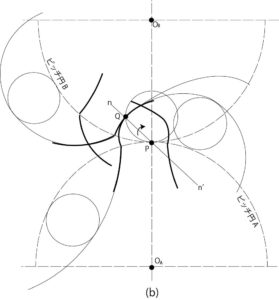
図9-b:サイクロイド歯形による伝動
図9-bのように2つの歯形曲線を点Qで接触させて法線\(n-n’\)を引くと、必ずピッチ円の接触点Pで円の中心\(O{_A}O{_B}\)を結ぶ曲線と交わるため、角速度比は一定になる。接触点の軌跡は弧\(\stackrel{\frown}{PQ}\)となる。





















